One of my favorite theoretical shapes is the möbius strip. Named after August Ferdinand Möbius who, concurrently with Johann Benedict Listing, discovered the shape.
A continuous closed surface with only one side; formed from a rectangular strip by rotating one end 180 degrees and joining it with the other end.
Princeton University
I really like mobius strips due to their simplicity. The geometry can be pretty quickly created in Grasshopper, within Rhino 3D. I wrote a script that allows me to get a slicable .stl file in minutes.
I have 3D printed a couple of mobius strips. Below is the largest.



For college I made a mobius fidget spinner, as an exercise to use the 3D printers. We had to create a spinner using the three nuts seen inset below.


There is an unintended feature of this fidget spinner. The geometry naturally causes a really cool optical illusion. The edge rolls over in only one direction.
Grasshopper Definition
I created a Grasshopper 3D definition to produce 3D models of mobius strips. I can control by the selections below, outer radius, inner radius, thickness, and rotations. There are a few more variables that are buried in the code.
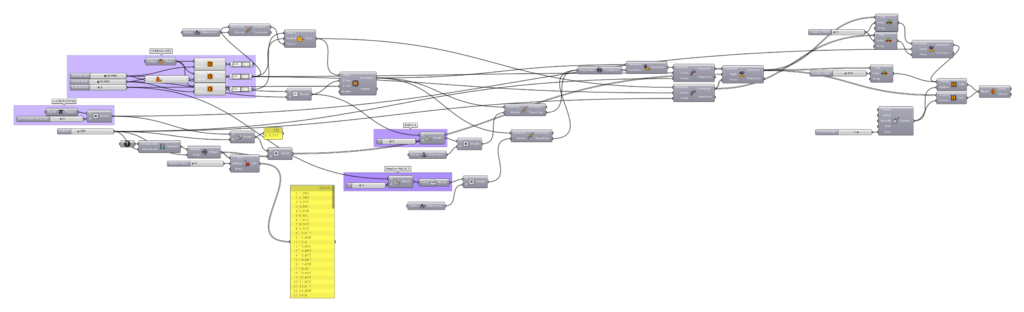
This seems to me like a great introduction to Grasshopper. My script works as follows:
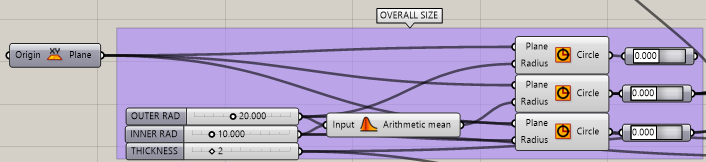
Step 1
The first step is to define the overall size of the calculated Mobius strip. Here we define 3 circles, all directly on the XZ plane.
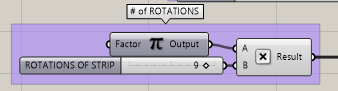
Step 2
Here is where we can set the number of rotations the strip will do.



University of Virginia Architecture
Finding interesting Grasshopper definitions is always a treat. The University of Virginia Architecture program has an awesome website sharing many definitions.

Leave a Reply